Attention-based networks have been shown to outperform recurrent neural networks and its variants for various deep learning tasks including Machine Translation, Speech, and even Visio-Linguistic tasks. The Transformer [Vaswani et. al., 2017] is a model, at the fore-front of using only self-attention in its architecture, avoiding recurrence and enabling parallel computations.

To understand how the self-attention mechanism is applied in Transformers, it might be intuitive from a mathematical perspective to build-up step-by-step from what is known, i.e. Recurrent Neural Networks such as LSTMs or GRUs to a self-attention network such as Transformers. Blog posts such as Jalammar, The Annotated Transformer, Vandergoten have attacked the explanation of Transformers from different perspectives but I believe this article will give another perspective and help engineers and researchers understand Self-Attention better, as I did.

For a beautiful explanation of everything Attention, check out Lilianweng post on Attention

Here’s what we will cover:

  1. Introduction
  2. Gated Recurrent Neural Networks
    1. What are these shortcut connections
  3. Gated Recurrent Units to Causal Attention
    1. Let’s free the dependent weights
    2. Let’s free up candidate vectors
    3. Let’s separate Keys and Values
    4. Let’s have multiple attention heads
  4. Gated Recurrent Units to Non-Causal Attention
    1. Let’s look at the entire input sequence
    2. Let’s give a sense of position to the attention mechanism
    3. Let’s use Non-Linear Attention
  5. Full Self-Attention Layer
  6. Conclusion

This article is based on a lecture given by Kyunghyun Cho at AMMI, 2020. Special thanks to him and his team for a beautiful NLP course.

Introduction

Recurrent neural networks with gates such as Long-Short Term Memory (LSTM) and Gated Recurrent Units (GRU) have long been used for sequence modelling with the advantage that they help to significantly solve the vanishing problem and long-term dependency problems popularly found in Vanilla RNNs. Attention mechanisms have also been used together with these gated recurrent networks to improve their modelling capacity. However, recurrent computations still persist.

Given a sequence of input tokens, $(x_1, x_2, …, x_T)$, where T is the total number of tokens. At time step $t$, we can calculate a hidden vector $h_t$ which is a representation of information gotten from tokens from time step $1$ to $t$.

Gated Recurrent Neural Networks

A key idea behind LSTM and GRU is the additive update of the hidden vector, $h_t \in \mathbb{R}^d$ with dimension, d

\begin{equation} h_t = u_t \odot h_{t-1} + (1 - u_t) \odot \tilde{h}_t \end{equation}

where $\tilde{h}_t$ is the candidate context vector for current time-step, $t$ which is gated and added to the previous context vector in a linear way. This allows information to be propagated from previous time-steps to the current time step, if necessary. As observed, the update gate, $u_t \in \mathbb{R}^d$

  • With $u_t \approx 0$ (zero vector), $h_t = \tilde{h}_t$ implying the candidate vector represents the new context vector, $h_t$, ignoring information from previous time-step.
  • With $u_t \approx 1$, (vector of 1s), $h_t = h_{t-1}$ implying the previous context vector is copied to the new time-step, discarding the candidate vector information
  • In most cases, $u_t$ will take values between $0$ and $1$, allowing some information depending on their values.

$\tilde{h_t}$ is a function of the current input, $x_t$ and the previous hidden vector, $h_{t-1}$.

$ \tilde{h_t} = f(x_t, h_{t-1}) = tanh(\textbf{W} x_t + \textbf{U}h_{t-1} + b)$ where $\textbf{W}$, $\textbf{U}$ are weight matrices, and $b$ is a vector.

Note that we have simplified the GRU update equations ignoring the reset gate.

An interpretation of the additive updates is that they help to create linear shortcut connections between the hidden vectors of the current state and previous states (similar to residual connections found in popular neural network architectures such as ResNet).

Shortcut connections between hidden vectors in GRU

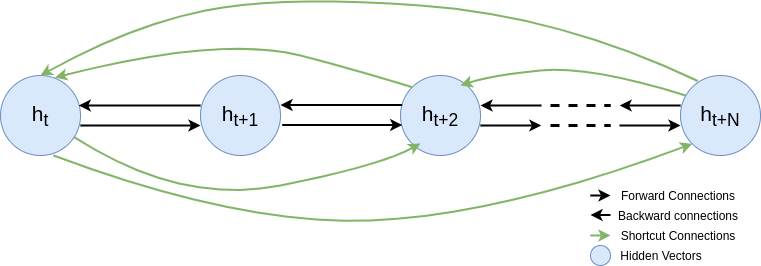
What are these shortcut connections

If we begin to unroll the hidden vector equation, moving step by step backwards, to extract the computations done to arrive there, we notice that it forms a weighted combination of all previous hidden vectors.

\begin{equation} h_t = u_t \odot h_{t-1} + (1 - u_t) \odot \tilde{h}_t \end{equation}

\begin{equation} h_t = u_t \odot \left(u_{t-1} \odot h_{t-2}+(1-u_{t-1})\odot \tilde{h}_{t-1}\right) + (1-u_t)\odot\tilde{h}_t \end{equation}

\begin{equation} h_t = u_t \odot \left(u_{t-1} \odot \left(u_{t-2} \odot h_{t-3}+(1-u_{t-2})\odot \tilde{h_{t-2}} \right) + (1-u_{t-1})\odot \tilde{h}_{t-1}) \right) +(1-u_t)\odot\tilde{h}_t \end{equation}

\begin{equation} … \end{equation}

\begin{equation} h_t = \sum_{i=1}^t \left(\prod_{j=1}^{t-i+1} u_j \right) \left(\prod_{k=1}^{i-1} (1-u_k) \right) \tilde{h}_i \end{equation} for $t$ steps of GRU update. The breakdown of $h_t$ shows the computation involving weighted combinations of all GRU’s previous states.

Gated Recurrent Units to Causal Attention

In causal attention as in GRUS, we will only have access or look at previous hidden states. This will allow us to proceed with our decomposition, but will be relaxed later to give a general non-causal attention.

Looking at the expanded version of the GRU update, we see dependencies between a lot of parameters and components. We will attempt to free these dependencies one-by-one given rise to a disentangled unit.

\begin{equation} h_t = \sum_{i=1}^t \left(\prod_{j=1}^{t-i+1} u_j \right) \left(\prod_{k=1}^{i-1} (1-u_k) \right) \tilde{h}_i \end{equation}

Let’s free the dependent weights

Recall that the update gate, $u_t$ is calculated thus in GRUs;

\begin{equation} u_t = \sigma(W_x x_{t-1} + U_h h_{t-1} + b_u) \end{equation} \begin{equation} h_t = f(h_{t-1}, x_{t-1}) = u_t \odot \tilde{h_t} + (1-u_t)\odot h_{t-1} \end{equation} where $W_x$, $U_h$ are weight matrices of the Update gate computation, $b_u$ is a bias vector and $h_t$, $x_t$ are hidden and input vectors respectively.

From both equations, we can observe that $u_t$, the current update gate is dependent on $h_{t-1}$, the previous hidden vector and vice-versa. To disentangle $u_t$ from $h_{t-1}$, we can learn the current hidden context, $h_t$ as a weighted combination of candidate vectors, $h_i$.

\begin{equation} h_t = \sum_{i=1}^t \alpha_i \tilde{h}_i \end{equation} where $\alpha_i \propto exp\left(ATT\left(\tilde{h}_i, x_t\right)\right)$ and $i$ ranges from time-step $1$ to the current time-step, $t$, implying that it uses the candidate vectors of all previous and current state to evaluate the hidden vector.

Let’s free up candidate vectors

Recall that $\tilde{h} = f(x_t, h_{t-1})$

where $\tilde{h_t}$ depends on $h_{t-1}$; $h_{t-1}$ depends on $\tilde{h_{t-1}}$ and $h_{t-2}$ and so on - check unrolled $h_t$ above.

This implies that $\tilde{h_t}$ still depends on all the previous $\tilde{h}_{t-N}$ candidate vectors.

To break these dependencies in candidate vectors, $h$, Recall that; \begin{equation} h_t = \sum_{i=1}^t \alpha_i \tilde{h}_i \end{equation} we replace the candidate vector by an input function $f(x_i)$. This input function takes in $x_i \in \mathbb{R}^d$ and map it into a space of $\tilde{h}_i \in \mathbb{R}^d$, without having to explicitly use previous candidate vectors.

The input function $f(x_i)$ which have been used to disentangle the candidate vectors for each time-step can serve different purposes as we see in Transformers.

  1. It is sometimes used to query which of the previous hidden states are important, i.e.

    $\alpha_i \propto exp\left(ATT\left(f(x_i), f(x_t)\right)\right)$

    where $i$ ranges from $1$ to $t$, $f(x_i)$ represents the Key vector and $f(x_t)$, the Query vector of the attention function, $ATT(., .)$. This attention function provides relatively high $\alpha_i$ values for $f(x_i)$ values associated with current token, $f(x_t)$.

  2. As seen, it is also used to calculate the candidate vectors for the content update i.e.

    $h_t = \sum_{i=1}^t \alpha_i f(x_i)$

    where $f(x_i)$ serves as the Value vector here.

    In summary, pass in a vector of input $x_i$ or $x_t$ to function $f(.)$ depending on what is required to calculate Query, Key and Value.

  • What is $f(x_t)$ or $f(x_i)$ ?

    $f(.)$ is a function that processes the current input $x_t$ or previous hidden vectors, $x_i$. At the input to the encoder or decoder, if $x_t$ or $x_i$ is a one-hot vector representation of a token, $f(.)$ is a lookup table or embedding layer. If $x_i$ is a hidden state from the lower layer, $f(.)$ can either be an identity function or a MLP.

Even though we have performed a lot of disentanglement, notice that Key, Value and Query vectors will be similar as they are derived from the same function.

Let’s separate Keys and Values

Instead of using a single linear function, let’s apply independent but similar linear functions to each of Keys, Values and Queries. These will just be 3 neural networks, $K$, $Q$, $V$ with independent weights. So we have;

  • the Key vector network, $K$ and Query vector network, $Q$ used in the attention function, $ATT$ to calculate the attention weights, $\alpha_i$

    $\alpha_i \propto exp(ATT(K(f(x_i)), Q(f(x_t))))$

  • the value vector network, $V$ used to calculate $h_t$,

    $h_t = \sum_{i=1}^t \alpha_i V(f(x_i))$

Putting it another way, we compute the attention weights, $\alpha_i$ by comparing the query vector of the current position, $Q(f(x_t))$ against all the key vectors of the previous inputs, $K(f(x_i))$, then compute the weighted sum of the Value vectors of all the previous inputs, $V(.)$ to get the hidden vector, $h_t$ at time-step $t$.

At this stage, we have pretty much built a disentangled model but ehrmm, we have only a single attention mechanism. Will this be enough to model all the dependencies in context/hidden vectors? Maybe, it will be a good idea to have multiple attention heads. What do you think?

Let’s have multiple attention heads

We can create N multiple possible $Q$, $K$ and $V$ functions/neural networks. Since each of them takes in the same $x_i$ or $x_t$, we can have parallel computation performed by each $Q$, $K$ and $V$ functions.

For each attention head, $n \in 1, 2 , 3,…, N$, we calculate $h_t^n$. Each $h_t^n$ is concatenated together to form the new $h_t$ i.e.

\begin{equation} h_t = \left[h_t^1;~ h_t^2;~ …;~ h_t^N \right] \end{equation}

where

$h_t^n = \sum_{i=1}^t \alpha_i^n V^n(f(x_i))$ and $\alpha_i^n \propto exp(ATT(K^n(f(x_i)), Q^n(f(x_t))))$

Questions?

  • Why concatenate the multiple attention heads instead of adding them, or use some other methods? Well, the concatenation gives a vector with a representation that provides information about different aspects of the inputs, and allows each head to specialize in attending. I don’t have an answer for that, if you do, please leave it in the comment section.

Gated Recurrent Units to Non-Causal Attention

We have previously only attended to previous and current hidden states in our network. In non-causal attention, we relax this assumption and we are allowed to also look at positions $t+1$ to $T$ of the sequence.

Let’s look at the entire input sequence

Since we have broken all the dependencies of candidate vectors and attention weights of all hidden states from $t = 1, …, T$, at time-step/position, $t$, we can utilize the previous hidden states, current hidden state as well as future hidden states. I prefer to call $t$ position now that there are no recurrent computations really.

$h_t$ then becomes; \begin{equation} h_t = \left[h_t^1;~ h_t^2;~ …;~ h_t^N \right] \end{equation}

where $h_t^n = \sum_{i=1}^T \alpha_i^n V^n(f(x_i))$

and $\alpha_i^n \propto exp(ATT(K^n(f(x_i)), Q^n(f(x_t))))$

Great!!, now we have a more robust attention mechanism. One problem still persists though. With this mechanism, we can just permute the order of the hidden states and nothing changes. Is that the behavior we want? Hmm, No!

Let’s give a sense of position to the attention mechanism

We can do this by adding a position encoded vector, $p(i)$ (usually of same dimension) to each input. Each $p(i)$ comes from a positional embedding $p$. This positional embedding is independent of the actual token embeddings.

So $h_t$ becomes;

\begin{equation} h_t = \left[h_t^1;~ h_t^2;~ …;~ h_t^N \right] \end{equation}

where

$h_t^n = \sum_{i=1}^T \alpha_i^n V^n(f(x_i) + p(i))$

and $\alpha_i^n \propto exp(ATT(K^n(f(x_i)), Q^n(f(x_t) + p(i))))$

$p(i)$ is the position encoded vector for position $i$ from positional embedding $p$.

Learned positional embedding and function-based positional embedding (such as sinusoidal positional embedding) are the common positional embeddings. The Transformer uses the sinusoidal positional embedding due to the property that it can generalize to lengths not seen during training.

To this point, we have only been using linear projections as our functions. Do you think a sprinkle of non-linearity will help our model?

Let’s use Non-Linear Attention

As seen from our discussion, we can extract the following about the linearity of our Attention. With

\begin{equation} h_t^n = \sum_{i=1}^T \alpha_i^n V^n(f(x_i) + p(i)) \end{equation}

  • the hidden vectors calculated through attention are inherently linear and are just weighted sum of input vectors.
  • Also, $f(.)$ is often an identity function (especially for intermediate layers)
  • p, the positional embedding does not depend on the input.
  • the Values vector network, V is often a linear transformation.

With the following observations, it will be difficult for the attention to manipulate the attention weights to find a complicated combination. The solution will be to apply a post-attention non-linear function.

Let’s define $g(.)$ as the post-attention non-linear function, which is a feed-forward neural network in our case, applied to each time-step independently.

\begin{equation} h_t = g\left(\left[h_t^1;~ h_t^2;~ …;~ h_t^N \right]\right) \end{equation}

For higher efficiency, $g$ may be applied to each head independently. $h_t$ becomes;

\begin{equation} h_t = \left[g(h_t^1);~ g(h_t^2);~ …;~ g(h_t^N) \right] \end{equation}

This gives us the Non-Linear, Non-Causal, Positional Attention used by Transformer.

It has been a long ride. If you have got this far, you are a Genius!! You must have gotten something from the article. Let’s bring all together in one place.

Full Self-Attention Layer

In summary,

  • the context vector with a single attention mechanism is calculated thus; \begin{equation} h_t^n = \sum_{i=1}^T \alpha_i^n V^n(f(x_i) + p(i)) \end{equation}
  • which are then concatenated together, either before or after applying a nonlinear function \begin{equation} h_t = g\left(\left[h_t^1;~ h_t^2;~ …;~ h_t^N \right]\right) \end{equation} or \begin{equation} h_t = \left[g(h_t^1);~ g(h_t^2);~ …;~ g(h_t^N) \right] \end{equation}
  • then, the attention weight are calculated using the Key and Query vectors as well as positional encoding for the input \begin{equation} \alpha_i^n \propto exp(ATT(K^n(f(x_i) + p(i)), Q^n(f(x_t) + p(i)))) \end{equation}

Conclusion

In this article, we showed how we can move from a recurrent-based neural network with gates such as GRU to a self-attention based model such as Transformer with disentangled hidden states and weights, enabling parallel computations.